As a wise man once said, there are as many rules of music engraving as there are music engravers. This is a joke, of course, but perhaps only half of one: although there are certain aspects of how music notation should be presented that more or less everybody can agree on, there are many more that provoke lively debate.
One of these latter areas is beaming; specifically, the placement of beams relative to stave lines, and the amount of slant or slope that should be applied to beams given notes of different pitches, the amount of horizontal space occupied, and so on.
Advance warning: this post goes into a lot of detail about subtle aspects of engraving practice concerning beam placement. Engraving nerds only need apply.
Evolution of beams
Beams first appeared in music notation around the turn of the eighteenth century, and trace their ancestry through the flags used to denote the rhythmic duration of shorter notes, and before that to the ligatures that denoted multiple notes to be sung to the same word or syllable, as shown in the now outmoded practice of beaming notes in vocal music according to the underlay of the words in preference to the rhythmic groupings of the meter. Beams are, simply put, compound flags: instead of drawing individual curly tails at the ends of the stems of successive notes, notes are joined by one or more thick lines. It quickly became standard practice to beam notes together according to the rhythmic groupings of the meter, and the result is music that is both much less visually cluttered (because beam lines are much less fussy than curly tails) and more strongly communicates the rhythms.
To illustrate how the engraving of beams has evolved over the past 300 years, consider the opening four bars of Sonata 1 from Arcangelo Corelli’s volume of 12 trio sonatas, Opus 2. Here is how British music publisher John Johnson rendered this music around 1720:
(You can click on all of the images in this post to view them at a larger size.)
All of the stems of the notes in the beamed group are drawn at (more or less) the standard length of 3.5 spaces, or an octave, and in their standard directions (e.g. the final A of bar 3, and the first D of bar 4 in the continuo part). The beam is simply drawn to join them, so that the beam has a concave or convex curve to it, or has an elbow if the stem direction of the notes changes within the beamed group. The beam line is also only moderately thicker than the width of the stem, and there is no evident consideration for where the stem tip ends up relative to the stave lines.
Here, by contrast, is how the German publisher Schott rendered the same music nearly 250 years later, in its Urtext edition of 1966:
Beam lines are now significantly thicker than the stems of notes and the stave lines; in fact, they are now half a space thick (and although this particular example does not contain notes shorter than an eighth (quaver), additional beam lines are typically separated by a quarter of a space). The beams no longer curve inward or outward by following closely the contour of the notes in the beamed group; instead, the beam either slopes upwards, downwards, or is horizontal, and the stems of the notes within the group are lengthened or shortened to meet the beam. The notes that caused beams with elbows in Johnson’s edition have had their stem directions reversed, so that the stems of all of the notes within the group have a consistent direction, allowing the beam to be positioned below the stave for those two groups. The beams that lie within the stave (the second group in the first bar, and the second group in the last bar) are carefully positioned relative to the stave lines to avoid small triangular gaps at the start and end of the beam, known as wedges. The beams are overall slanted less steeply, and there is a pleasing balance to the appearance of the music.
Three steps to (beaming) heaven
There are at a high level three distinct processes that go into determining beam placement: firstly, working out the stem directions of the notes in the beamed group; secondly, determining whether the beam should slope upwards or downwards, or should be horizontal; and thirdly, determining the final stem lengths required to produce a beam that is correctly positioned relative to the stave lines, with the desired slant.
Two of the beamed groups in the Corelli example nicely demonstrate the decisions to be made regarding the stem direction of notes in beamed groups. Look, for example, at the second beam group in bar 3 in the continuo part: G3, E3, and A3 should all take down stems; A2 should take an up stem. In this case the majority of notes take down stems, so the group overall takes a down stem. The first group of bar 4 is similar: the first D3 may take either an up or down stem because it is on the middle line of the stave; however, D4, C#3 and A3 all take down stems. Again, the majority of notes take down stems, so the group overall takes a down stem. In the case that an equal number of notes take each stem direction, the stems may all point up or down; to make this decision, you might consider whether the beam groups to either side of the indeterminate group have stems pointing up or down and choose to follow them; or you could simply choose to make the stems point down, which is the default choice in the absence of anything to the contrary.1
Whether the beam should slope upwards or downwards, or be horizontal, is determined by the stave positions of the first and last notes in the beamed group: if the first note is lower than the last note, the beam slopes upwards; if the first note is higher than the last note, the beam slopes downwards; if the first and last notes are at identical stave positions, the beam is horizontal. The beam is also horizontal if the notes in the group are in a repeated pattern of pitches; or if all but one of the notes in the group are the same pitch, and the note of differing pitch is furthest from the beam; or if the notes in the middle of the group are closer to the beam than the notes at both ends of the group (called a concave beamed group).
While there is little debate over either of these first two processes, when it comes to choosing the final stem lengths that determine both the position of the beam line or lines relative to the stave lines and the amount of slant in the desired direction, there is considerably less agreement.
The book that provides the most detail on this subject is The Art of Music Engraving and Processing by Ted Ross2; both Elaine Gould’s Behind Bars and Kurt Stone’s Music Notation in the Twentieth Century provide a summary of Ross’s rules. Ross is considered so authoritative in this regard that engravers refer to “Ross beams”, referring to beam positions that broadly follow his recommendations. Frustratingly, despite devoting nearly 50 pages of his roughly 300 page book to beaming, there is still plenty of room for debate.3
A lot of the complication with beam placement comes from what Ross calls the “cardinal rule”:
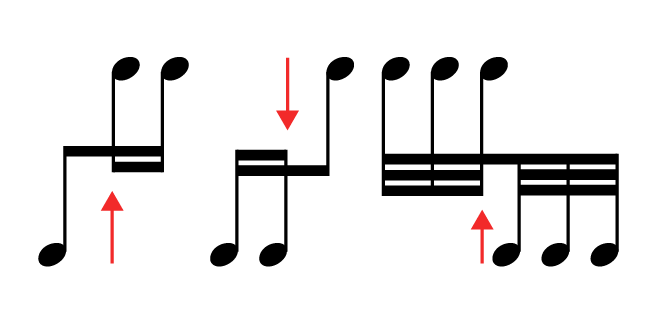
The placement of a beam follows the cardinal rule that when it falls within the staff, its ends must either sit [on], hang [from], or straddle a staff line, whether the beam is single or multiple.
Normally, an unbeamed note’s stem is 3.5 spaces long, with the stem tip an octave away from the notehead, though notes on more than one ledger line above or below the stave have their stems extended such that their tips meet the middle line of the stave. A beamed note’s stem may be shortened or lengthened in order to produce both the correct placement relative to a stave line, and the correct amount of slant.
There is no agreement on what constitutes the correct amount of slant (even within the pages of Ross’s own book his examples are inconsistent), but the general principle is that the amount of slant, determined by the vertical positions of the stem tips of the first and last notes in the beam, is determined by the difference between the stave positions of the first and last notes in the beam. In well-engraved music, the smallest slant, for beams whose first and last notes are separated by one stave position (an interval of a second), is typically 0.25 spaces (i.e. the stem tip of the last note in the beam is 0.25 spaces higher or lower than the stem tip of the first note in the beam), and the maximum slant, for beams whose first and last notes are separated by seven or more stave positions (an interval of a seventh or more), is typically between 1.25 and 1.75 spaces.
Because the angle of a straight line between two points is greater as the two points move closer together, well-engraved music tends to use smaller differences between the positions of the stem tips to produce shallower angles when notes are closely spaced, up to a maximum difference of 0.5 spaces. Gould further suggests that a beamed group consisting of only two notes should never have a slant exceeding 0.5 spaces, regardless of the space between them.
Generally speaking, then, attractive beam slants are relatively shallow, rarely exceeding two spaces even when the intervals between the first and last notes under the beam are very large.
The actual slant that is produced may differ from the ideal slant, however, in order to ensure that the stem tips are placed correctly relative to the stave lines: as Ross’s cardinal rule states, each end of a beam must either sit on, hang from, or straddle a stave line. Furthermore, no beam should be closer to a notehead than two spaces, which means that as more beam lines are added (as the duration of the beamed notes get shorter), the natural tendency is for stems to get longer. The exact stem length of the notes in the middle of a beamed group is dictated by the slant of the beam, but the beam itself must take into account the stave positions of those notes to ensure that the beam line or lines do not end up too close to the notes in the middle of the beam.
So a little tug of war must be resolved for every beam group: the stem tips of the first and last notes should be positioned to either sit on, straddle or hang from the stave line, and the stems of the intervening notes under the beam should be sufficiently long to avoid the beam lines getting too close.
Different scoring applications resolve this tug of war in different ways, which is illustrated in the picture below: open it in a new tab or window to see the whole picture.
As a reminder, Product A and Product B are the leading commercial scoring programs, Product C is an open-source engraving program that uses text input files to compile PDF output, Product D is a venerable commercial engraving program dating from the MS-DOS days but still used today by some publishers, and Product E is a popular open-source scoring program with a graphical user interface.
There are three rows of annotations below each example: the first row describes the placement of each end of each beam, using the abbreviations S for sit, St. for straddle, H for hang (the same convention used by Ross in his book), and in a couple of places where the stem tip does not seem to be following any specific placement, ?; the second row gives the length of the stem at each end of each beam, in stave spaces; the third row describes whether the beam is flat (F), slopes upwards (U), or slopes downwards (D), and if it slopes, by how much, again in stave spaces.
Looking at these examples is somewhat instructive. Broadly speaking, all of the various products produce similar default results, but there are some subtle if significant differences.
Product A, for example, by default shortens the stems of all beamed notes by 0.25 spaces, presumably to allow a wider range of placements, while Product B never allows any stem within a beamed group to be shorter than 3.5 spaces, which produces generally longer stems than necessary in many beamed groups, and also never produces slants of less than 0.5 spaces, which means that beams only ever sit or hang, and never straddle. Product B also produces flat beams in more cases than other programs, due to the default choice of beaming style set in its default document. Experienced users of Product B tend to rely on a third-party plug-in to produce stem lengths and beam slants closer to those recommended by Ross, though this of course has the disadvantage that the plug-in has to be run again if the score is edited further after running the plug-in for the first time.
It’s also notable that both Product A and Product B produce very similar slants for beamed groups of varying intervals: Product A produces a slant of 1 space for an interval as small as a fourth and as large as a seventh, and a slant of 0.5 spaces for an interval as small as a third; Product B produces a slant of 0.5 spaces for all sloping beams in this particular example. Ross’s recommendations are for the slant to increase somewhat as the interval between the notes at either end of the beamed group widens.
Product C generally produces pleasing beam slants for this example, though it is curious that it aggressively shortens the stems of the notes in the final beam group, to the point that the stem of the final note is at the minimum length allowed by Ross (2.5 spaces), which makes that group’s beams look particularly stubby.
Product D also produces pleasing beam slants, though it is curious that the beam group describing an interval of a fifth produces a larger slant than the group describing an interval of a seventh, in which the first stem is unnecessarily lengthened and indeed is the only stem tip not to be placed in a sit, straddle or hang position relative to an imaginary stave line below the bottom of the stave (other programs tend to continue placing beams as if there are additional stave lines above or below the stave, as this helps produce more consistent slants regardless of the stave positions of the notes under the beam). Again, experienced users of Product D typically rely on a third-party application that post-processes the default results using enormous numbers of look-up tables for predefined slants based (presumably) on different combinations of numbers of notes in the beamed group, number of beam lines, and position on the stave.
Product E encounters a similar problem with the sixth beam group to Product D, again producing a placement for the first stem tip that neither sits on, straddles nor hangs from the first putative stave line below the stave. It also chooses not to reduce the length of the last stem in the beamed group, so this beamed group also protrudes unnecessarily far from the stave; only Product B, which never allows stems to be shortened from their default length, produces a similarly large protrusion (though it also produces no slope for this group, which is arguably the more problematic aspect of its result).
Our application produces a slightly wider range of slants than the other products in the comparison: the smallest slant it will produce is 0.25 spaces, for an interval of a second, and the largest is 1.5 spaces, for an interval of a seventh or more. Of course, the values for the optimal slant for beamed groups describing each interval from a second up to an octave will be adjustable by the user to suit individual taste or a publisher’s specific conventions.
This comparison illustrates that there is a great deal of variation in how beam slants are calculated, even with very simple beam groups consisting of only a single beam line. Only an engraver with a keen eye would perhaps take serious issue with any of the beams produced by these applications, with the exception of those produced by Product B, which are by some distance the furthest away from the recommendations in Ross’s book.
Beams between staves
When beams are positioned between the two staves of a keyboard instrument, one of the special considerations is how to handle changes in the duration of the notes under the beam. Additional beam lines can be placed on either side of the primary beam line, but if they are placed on the wrong side, they create unsightly beam corners, as illustrated below.
The comparison below shows how different scoring programs handle cases that are liable to produce beam corners.
Product A produces beam corners for all four examples; Product B appears to have a policy that subdivisions are always placed above the primary beam, which means that it is correct some of the time and incorrect the rest of the time (in this example, the first two beams happen to be incorrect, and the second two happen to be correct); Product E, by comparison, appears always to place subdivisions below the primary beam, so it, too, is correct some of the time and incorrect the rest of the time.
Only our application and Product C correctly handle beams that would otherwise produce beam corners. They can normally be avoided by placing additional beams on the stem side when all the stems of the same subdivision are in the same direction, and when the outer stems of the same subdivision are in the same direction.4
Beaming grace notes
As I mentioned earlier, despite spending more than 50 pages of his book talking about beams, Ted Ross doesn’t manage to settle any arguments about beam slants. One aspect that goes completely undiscussed, for example, is how to handle beamed groups of grace notes, and indeed neither Gould, nor Stone, nor Gerou and Lusk weigh in on this issue, either.
Grace notes are particularly challenging because they are smaller than normal notes – typically around two thirds or three fifths the size of normal notes – and as such, noteheads, stems, and beams are all scaled down together. Normally, a beam line is 0.5 spaces thick, and is separated from its neighbour by a gap of 0.25 spaces, but when a beam line is scaled down for a grace note, it becomes around 0.3 spaces, and the gap betwixt it and its neighbour becomes 0.15 spaces.
This makes placement of stem tips relative to sit, straddle or hang positions on stave lines challenging, particularly since the distance between stave lines is relatively much larger than for normal notes, which means that if both ends of the grace note beam are going to be placed correctly, the beam slant must either be shallow (e.g. hang to straddle, straddle to sit, or hang to sit, all relative to the same stave line), or quite steep (e.g. hang from one stave line to hanging from the stave line above or below).
Most existing applications make no attempt to produce good placement for groups of beamed grace notes, as can be seen below.
Product A, Product B, and Product E all take an apparently simplistic approach to positioning beams on grace notes: everything is scaled down by the grace note scale factor, and the stem tips are allowed to fall where they may. This sidesteps the issue of requiring the slants to be either shallow or steep, but does mean that wedges are much more likely to occur; wedges are arguably more problematic for grace note beams than normal-sized beams, since the gap between the beam lines is proportionally smaller and thus easier to fill in with a stave line. However, Product A and Product B do appear to set limits on the amount of slant that can be produced for grace notes, which would in itself be something of a protection against wedges, if only the stem tips were correctly positioned relative to the stave lines, which they are not. In addition, neither Product A nor Product E appear to correctly enforce the rule that no beam line should be closer to a notehead than two spaces (or around 1.2 spaces at the grace note’s reduced size), e.g. the penultimate beam group for Product A, and the second bar for Product E, which also features beam slants that are probably too steep for anybody’s taste.
Product C takes a different approach: it does produce good placements for the stem tips of the first and last notes in a beamed group of grace notes, but it also increases the size of the gap between the beam lines. In fact, the separation of beam lines is only fractionally narrower for grace note beams than it is for normal beams. This has the advantage of making the problem of wedges no more or less serious than it is for beamed groups of normal-sized notes, but has the disadvantage of making beamed groups of grace notes have practically the same colour (or overall blackness) as normal-sized notes.5
Our application does produce good placements for beamed groups of grace notes, and also limits the amount of slant allowed for a group of only two notes, which helps to avoid very steep slants for beamed groups that are naturally narrowly-spaced. For beamed groups with more than two notes, the stem tip of the note at each end of the group snapped to a valid placement relative to the appropriate stave line. This approach gives results that are very close to traditionally-engraved scores from before the age of computer engraving.
Shearing vs. rotating beams
Most applications draw a flat beam by drawing a rectangle of 0.5 spaces in height. When a sloping beam is required, most applications simply offset the two points at either or both ends of the rectangle by the required vertical distance, making a parallelogram, a kind of transformation known as shearing. This makes the beam line appear progressively thinner as the slant increases, which you can see in this example:
Most applications handle beams this way because it is unusual for beams to have a slant exceeding two spaces, and at small to moderate slants, the effect of the thinning of the beam line is not particularly noticeable.
However, this is not how beams were handled in the days before computer engraving: in traditional engraving, the engraver would use a tool of the appropriate width, and rotate it to match the slant of the beam before making his mark on the plate. As such, beam lines in traditionally-engraved music are always truly half a space thick, regardless of their slant.
We always strive to match even the smallest details of pre-computer engraving, and as such our application rotates beams in the same way that a human engraver would rotate the beam tool, so that the thickness of the beam line is always 0.5 spaces along its whole length, giving a greater visual consistency to the colour of beamed groups with different slants.
You can see the difference between shearing a beam line and rotating it properly in this image.
To our knowledge, no other application does this by default6, and it’s another example of the attention to fine detail that runs through all of our work.
Widening beam gaps for very short notes
Another subtle but important detail concerns the treatment of beamed groups of notes requiring three or more beam lines, i.e. 32nd notes (demisemiquavers) or shorter durations. Because three beam lines add up to a total height of two stave spaces (3 x 0.5 space lines, 2 x 0.25 space gaps), this limits the range of slants that will produce valid beam placement. As Gould says:
With the addition of a third beam, the beams must slant a whole stave-space. Any other angle will result in one of the beams beginning or ending in the middle of a stave-space, which is less than satisfactory.7
She goes on to recommend that the distance between beams should be widened slightly in order to allow for a slant of less than one stave space.
Few existing scoring programs widen the gap between beam lines for beamed groups of 32nd notes or shorter by default, as can be seen from the comparison image below of groups of 64th notes (hemidemisemiquavers).
Notice that even for a flat beam, Product A, Product B, and Product D produce poor beam placement, with the stem tips of the notes at either end of the beamed group floating in the middle of a stave space. This is a consequence of not increasing the gap between each beam line: with four beam lines separated by gaps of 0.25 spaces, no correct placement within the stave is possible. Our application, together with Product C and Product E, increase the gap between the beam lines, and thus produce correct placement.
Although Product A follows the recommendation that beamed groups of 32nd notes within the stave should produce a slant of 1 stave space, for 64th notes it allows smaller slants, with the second beamed group in particular (with a slant of 0.25 spaces) producing especially prominent wedges.
Product E consistently follows the recommendation for both 32nd and 64th notes, with the result that it produces a slant of 1 space for both the second and third beamed group; however, it does not ensure the correct amount of minimum space between the innermost beam line and the notehead at the right-hand end of the beam; the correct placement for this beam would be for both stem tips to extend by one additional stave space.
Product C and Product D both produce flat beams for all three of these beamed groups. For 32nd notes, Product C produces slants that do not ensure correct beam placement, despite widening the beams correctly. Product D does not widen beams for either 32nd or 64th notes, and produces no slants for 64th notes, but does produce a slant for large intervals for 32nd notes; however, it does not produce a slant of one stave space, so the placement of the beam relative to the stave lines is incorrect.
In various situations involving slanted beam groups with 32nd notes and shorter durations, therefore, Product A, Product B, Product C and Product D all produce beam placements that result in the stem tip of the note at one or other end of the beamed group landing in the middle of a stave space, which should be avoided wherever possible.
Only our application actually widens the gap between beam lines in order to produce both a smaller slant, the correct placement of the beam relative to the stave lines, and an appropriate minimum distance between the innermost beam line and the notehead closest to the beam. (It should be noted that it may not be to everyone’s taste to widen the gap between beam lines in this fashion, so this behaviour is of course optional, and if widening is disabled, our application still produces only valid slants of 1 space for groups of beamed 32nd notes and shorter durations where the beam is placed within the stave.)
In summary
This rather lengthy post has hopefully opened your eyes to some of the more subtle aspects of truly fine music engraving, and demonstrated that we are dedicated to producing output of the highest quality, upholding the traditions developed over the past three centuries, and ensuring that they are carried forwards for the musicians of the future.
There is, as always, much that could be said about many of the other things we’re working on, but that will have to wait for another instalment. Until then, beam me up.
- There are of course further subtleties here. For example, if one note in the beamed group is very high or very low in comparison with the other notes in the group, the stem direction of that outlying note should determine the stem direction of the beamed group, to avoid having a majority of notes with excessively long stems. There are many more similarly subtle rules, which you can read about in Behind Bars or The Art of Music Engraving and Processing. ↩
- Ross’s book is not available in print any longer, but a CD-ROM version can be purchased from NPC Imaging. ↩
- The Alfred Essential Dictionary of Music Notation by Tom Gerou and Linda Lusk deserves an honourable mention here, as the authors of that book take an admirably practical approach to this thorny issue. A lot of the complexity in Ross’s rules arise from attempting to avoid wedges, and they argue that with improvements in the consistency and fidelity of computer output, wedges are much less of an issue today than when using more traditional methods of engraving, and therefore do not recommend going to heroic efforts to avoid them. However, they also state that “adjusting many beams individually on the computer is very time-consuming,” which I interpret as the more significant factor in their recommendation. Certainly if you wanted to avoid wedges without it becoming very time-consuming, you would be well advised to choose your scoring application carefully! ↩
- See page 316 in Behind Bars. ↩
- Furthermore, I’ve not personally encountered any published editions that use such a large gap between beam lines for groups of beamed grace notes. Perhaps one of the developers of Product C dreamed this up; as a solution to the geometric problem it certainly has merit, but it is unusual. ↩
- Users of Product B can achieve this effect with the use of a third-party plug-in, though this carries with it all of the disadvantages of using plug-ins in general, such as needing to repeatedly re-run the plug-in after making further edits to the music. ↩
- See page 21 in Behind Bars. ↩


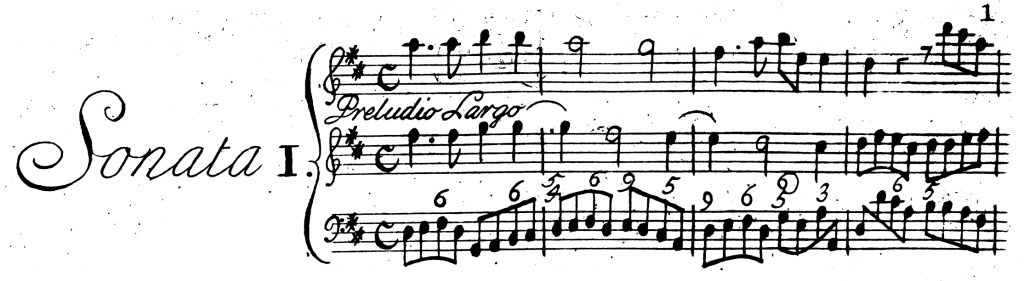







Extremely interesting reading, as always. Thank you for sharing again. When reading about “beam corners” I can’t help but link to this image. This is in no way a real-world example (well, it *is* from a real-world, published score, but an extremely rare case), but do you think your application will be able to produce such “abnormal” notation too?
@Urs: At the moment, no, our application can’t produce a beam looking like that. I’m not even sure I know how to interpret that notation.
My guess would be that it’s communicating two simultaneous phrasing concepts: 2 groups of 6 notes, as well as 3 groups of 4 notes.
The interpretation is pretty clear, a variant of a hemiola (think/play groups of four 16th notes while in a 6/8 time signature). Of course this notation is extremely uncommon and it is in no way relevant if an application can do that (except if your advertising “create anything you can imagine with XY” of course). However, again I can’t resist linking to this engraving example – which is (apart from some ingenious trickery regarding the beaming) automatic engraving out-of-the-box BTW.
I find that notation unbelievably confusing to read!
I’m not sure if you are referring to the original notation or to the engraving example. Well, the notation is a historical one that hasn’t established itself. And if you’re talking about the engraving you might want to browse that repository for the initial results some of the competitors provided – but I won’t continue this here, as we (I) have written too much OT already (sorry).
🙂
@Urs: People who are impressed by the engraving example might also want to take a look at the input file that produced it, and consider whether or not they consider this kind of hardcore encoding is something they would be willing or able to learn.
For some, of course, the trade-off of almost complete flexibility versus needing to learn how to program (and I believe this example does fall into the realm of programming rather than simply learning a text input syntax) is absolutely worth it, but for others (and, I would posit, for most) I believe the sacrifice of some small amount of flexibility for rarely-needed, non-standard notations versus a significantly easier to learn and potentially more efficient input method is one they will be happy with.
Daniel,
I was a bit hard on you and you rightly cut me down before when asking for better editing of cc automation than what Sibelius offered. After examining your competition, I feel compelled to remind you of how important this is for a v1.0 release.
Staff Pad – Expression Layer
Notion – The same thing
Cubase – The Piano Roll
Every DAW has this for a reason. Notation competitors added it for a reason. If that isn’t reason enough to take this feature request seriously enough for a v1.0 release, then consider this. There is absolutely no point in your program supporting VST and midi playback if there is not an easy way to edit the playback parameters. If Steinberg only wanted notation, VST wouldn’t be on the roadmap. With no disrespect to copyists everywhere, page magic and beaming doesn’t make written music. Composing does. Live playback is important. Mock-up quality also is. If I can use a notation editor as my mock-up tool I will. If I can’t, I’ll use Cubase. My point isn’t to say that you have the wrong approach. But if you have midi playback, allow people to edit “the midi playback”. Otherwise take it out, I’ll keep using Cubase and use the notation program when it comes time to print and for nothing more.
I think that’s a pretty fair way to describe this. Either do it right, or don’t do it.
To anyone else reading this. I’m playing hard ball. On purpose. I love Steinberg. I love Daniel’s posts. I’m beyond excited. I just want to see this program developed right from the start, not jerry-rigged together the way other notation software has been.
-Sean
Hemiola in 16th notes – showing 3/4 over the top of 6/8?
Just got introduced to Steinberg’s notation software. My most pressing need is for a program that can produce both staff notation and french baroque tablature. I’ve seen and used a number of programs, and all have their shortcomings. Steinberg, good luck with your software. Better notation programs are always appreciated.
Peter have you reviewed this software yet? http://lute.musickshandmade.com/
I have been using Finale music software to publish French Baroque lute tab for the viola da gamba. This process included creating a template and instruction. The result is quite acceptable, but time consuming. Contact me if interested.
Thanks as always for the fascinating insight! Crazily enough, last night I went to bed working on eliminating the “beam corners” in “Product E”, this morning I woke up with an idea for a solution, and then your blog popped up saying almost exactly what I was about to try out. Absolutely insane – especially considering there was a similar timeliness to your blog post on accidentals.
I guess you don’t post these specifically to help the competition :-), and probably many of the others aren’t in a position to be making changes in response to your comparisons, but we over here just eat this stuff up, so thanks again! BTW, we are on track for a release of 2.0 later this month; hopefully if you end up doing more comparisons like this, you’ll be able to use that.
I wish you great success on your work!
Great post, thanks Daniel! I’m really glad your team is paying attention to these details. However, I do have a disagreement about how Steinberg is handling the beaming in the example with the 64ths. The very reason many of these sit/straddle/hang beaming rules originated was to avoid forming the small white wedges which used to fill with ink when printing. (See Ross p98) That’s really no longer an issue, but they still seem unattractive to me after seeing so much quality engraving without them and your example is unnecessarily creating them. I disagree with Gould and think Ross’s solution is the preferred one here. Gould is saying “with the addition of a third beam, the beams must slant a whole stave-space” but look at Ross’s example on p125. His last example with 3 beams has the same issues as your middle group of 64ths, but his is much more elegant to my eye and avoids any of the wedges. Just my $0.02.
@Fred: Thanks for your comment. However, I’m not sure I follow your comment about the beam widening case. The last example of 32nd notes (three beam lines) on page 125, immediately before the “Section 11” heading, shows the same 0.5 space separation between beam lines, with a 0.25 space slant for the beamed group, which is exactly what our application produces in the same situation. At least as I read them, Gould’s recommendations and Ross’s recommendations for how to handle beamed groups of 32nd notes and 64th notes agree, and we are following them. However, as I wrote in my post, the beam widening behaviour is optional, so if you aren’t concerned about wedges in these situations, you can disable it.
Hi Daniel,
The example I took issue with was the second group of 64ths in your example. I (and Ross) disagree with your interpretation of Gould’s statement that the beam should slant a full space here. Having a full space slant (hang to hang) for an interval of a second just looks wrong IMO. Additionally it creates many wedges unnecessarily. Ross’s example on p125 is only 32nds, but if you turn the page upside down, he has the same interval as your second group of 64ths, yet by using straddle to sit his example creates no wedges.
Furthermore, if you look at Gould p21, she even supports Ross’s recommendation here in example (c) and states “In the past, to ensure both ends of all beams are attached to stave-lines, some editions have slightly widened the distance between beams to allow for an angle of less than a stave-space. This is a good compromise.” Here her example (c) uses Ross’s technique, creates no wedges, and is much more elegant to my eye.
Just to elaborate a bit more, I think it is the interval of a second that is what makes this so noticeable. Your solution is creating many more wedges than Product A for example, and having a beam slant more extreme than the interval just looks off to me. This is further complicated by the fact that for some reason you are having the closest beam always hang from the middle line when there is an angle, but not if it is flat. Having the second group start the beaming a full space lower than the first group, looks very odd in succession because it is the same note. Perhaps there is some justification for this, but I am not seeing it in either Ross or Gould.
@Fred: When a beamed group has three beam lines, you can separate the lines by 0.5 spaces, which means that each beam line plus its gap adds up to 1 space; this also means that all three beam lines will have the same placement relative to the stave lines when the beam is slanted. As such, you can slant a beam group with three widened beam lines by e.g. 0.25 or 0.5 spaces and still ensure that the beam has correct placement. If you don’t increase the separation between the beam lines from 0.25 spaces to 0.5 spaces, the beam slant cannot be less than 1 space without resulting in poor placement for one end of the beam or the other.
When a beamed group has four beam lines, the gap between the beam lines must be increased from the normal one quarter to one third of a space, so that the distance from the outside of the first beam line to the inside of the fourth beam line is three spaces (4 x ½ + 3 x ⅓). Gould discusses this on page 18. With a flat beam, each beam line is, to use Gould’s word, “attached” to a stave line, though only the outermost and innermost is technically placed exactly as it should be (i.e. in a sit or hang position); the inner two beam lines straddle in an approximate fashion, rather than straddling a stave line in the precise centre of each beam line. As a consequence, the only slant that will continue to produce this kind of arrangement is one that allows the stem tips of the notes at either end of the beam group to end exactly on a stave line; ergo, the only valid slant is one space.
As I wrote in my original post, widening the gap between beam lines may well not be to everybody’s taste. Since it has not typically been done in the age of computer engraving, it can look a bit odd to eyes used to reading music produced using the current generation of scoring applications. You may well feel that the trade-off of shallower slants versus correct placement of each end of the beam is worth making. We will provide an option to disable widening for beamed groups with three or more beam lines for this very reason.
Thanks again Daniel! I’m really glad you all are paying attention to a lot of the fine details other programs have glossed over. However, I still think that there is another possibility here even with 4 beams (which I very infrequently encounter IRL anyway). Ross p101 states “beamed notes with a difference of the interval of a second slant one-fourth space.” This is rubbing up against your software’s apparent rule of “there must be one clear stave-line between the innermost beam and the first ledger line” (Gould p19) in this example. Ross however allows for this particular example though on p126 stating “if the stems are pointed down a secondary beam can never be placed higher than the fourth line of the staff. (The beam may straddle in both cases.)” Using hang to straddle in this case would obey Ross’s rule over angle slant of one-fourth, would obey Gould’s rule that there must be a clear staff line, and would result in less wedges created than your example. Gould (and your software) is not allowing for the straddling option of the terminal that Ross is allowing for if I’m reading it correctly.
I came of age using Tom Brodhead’s BEAM program to alter SCORE’s beaming and then moved on to Finale and Sibelius. I haven’t used SCORE in a while but I’ll boot it up on my laptop later and see how they handle it. I’m genuinely curious at this point.
@Fred: Sorry to let this go cold for a little while: I was attending a conference the last couple of days. I have conferred with my colleague James about this issue, and we both think that you are mistaken that you could use a slant of 0.25 spaces with a beamed group of 64th notes, because one or other end of the beamed group must end in a space, as shown in this mock-up. This placement also causes at least one of the inner beams to form a wedge with its stave line. We maintain that the only valid slant for a beamed group of 64th notes with a widened gap is one space.
Our application does allow the innermost beam to straddle the second stave line in some circumstances, by the way (per Ross), but not currently in the situations shown in the example with the beamed groups of 64th notes.
Allow me to agree with the disagreement. I find the Steinberg solution here extraordinarily hard to read. There is so much visual clashing going on due to the slants on the 64th notes it’s almost like a moiré pattern.
@Tyler: As I’ve said numerous times now, the beam widening behaviour is completely optional, so if you don’t find it to your taste, you don’t have to use it.
Your examples don’t mention multi-note tremolos, but I assume that the considerations are similar. I wonder if the example that @Urs posted might be some sort of tremolo.
I think this weird beaming is intended to show the two levels of patterning going on: the primary beam shows the rhythmic groups of six (sextuplets), and the secondary beam the patterning of the pitches in groups of four, very perceptible in the fingers when one plays the piece. (Chopin Op. 25 No. 11). But I don’t believe I’ve ever seen such beaming before.
I enjoy reading your articles on notation. I like to print them so I can read them offline.
The graphics that are in the PNG format, like the comparison charts regarding beaming, all come out with a black backgroun. Not useful and wastes a lot of toner. Help! What can I, or you, do to fix this problem.
Thanks,
@Roger: I’m sorry you’re having problems with the PNG files. If you email me I can potentially send you PDF versions.
Maybe try “printing” to a PDF, and then printing that?
Which will this application work Operating Systems and versions? (win xp,vista,7,8+)
@ercan: We haven’t made any decisions about this yet, but in general Steinberg targets the current versions of Windows and OS X at the time of the release of a given version of each of our applications.
Whereas it’s quite correct and praiseworthy to aspire to the best possible notation, as far as I’m concerned the real question revolves around how readable it is, rather than how beautiful it looks. Almost all the above examples are perfectly readable without any likelihood of misinterpretation. I like the look of the Steinberg interpretation of beams, but I’d be perfectly happy with most of the others.
I’m rather reminded of the opinions in the 18th century surrounding the rivalry between Handel and Bononcini:
Some say, compar’d to Bononcini
That Mynheer Handel’s but a Ninny
Others aver, that he to Handel
Is scarcely fit to hold a Candle
Strange all this Difference should be
‘Twixt Tweedle-dum and Tweedle-dee!
Legibility is relatively easy to achieve — elegance is far more difficult. Yet in the world of music engraving it is the elegant which seems to survive far more than the merely legible and I have found that it is the elegant which is far easier and more desirable to perform from. I applaud Daniel and his team for taking the time to think through all these decisions about the tiny minutiae which make the difference between the merely legible and the truly elegant in computer music notation programs.
And I further applaud Daniel specifically for taking the time to prepare these postings which keep us informed about the progress of this new product from Steinberg. These keep those of us who are eagerly awaiting this new product aware of the ongoing development progress and issues, and allow us to keep up our hope. Too many products in the history of personal computers have been announced with great fanfare and then disappear into vaporware status, never to be heard from again. But Steinberg seems intent on keeping up the public awareness of this developing program, something rarely seen in software development, giving those of us who are still using the other commercial products or the marvelous freeware product with the graphical interface (I guess we shouldn’t be naming actual products here) great hope for the future.
Thank you Daniel for these posts!
Thanks for taking the time to write this blog! Very interesting to read.
There’s one thing I don’t agree on:
We needed to tackle this beam calculation as well, but if it was about sheared vs rotated beams we concluded that sheared beams are nice side-effect of computer-engraving.
Beams are 0.5 space thick, if you maintain this thickness on an angled beam the gap between multiple beams (16th notes) will become smaller until there’s no gap left. Therefore we think that shearing the beams is the better of two evils.
I quickly Photoshopped an example to visualize the problem.
@Hans: You do have to be careful with how you handle the separation of beam lines when rotating them rather than shearing them. We didn’t come to the same conclusion as you, but you can be sure that our rotated beam lines don’t eliminate the gap between each line in the way your screenshot shows.
I agree, but how are you going to maintain the Sit-Hang-Straddle rule if the gap between beams is highly variable?
@Hans: Prioritise correct placement of the stem tips, which ensures correct placement of the outer (primary) beam line, and then allow the inner beams to be positioned at slightly sub-optimal placements relative to the stave lines, because the full-sized gap is still employed. Because slants are limited to less than two spaces by default, the deviation in the placement of the inner beam lines is pretty small, and in our opinion, the benefits of consistency of colour outweigh the small inaccuracies in the placement of the inner beam lines.
A slant larger than 2 spaces is mostly bad engraving, but they do occur in high quality engraved scores. The beams I found with a slant larger than 2 spaces (in high quality scores, hand engraved) always appear above or below the staff-lines (just found out).
I wonder if there are situations where the sub-optimal becomes wrong, without being ridiculous off course.
I look forward to the day I can get to work with Steinberg’s new notation software. The level of detail you are putting into this is amazing. Keep it up!
I prefer Steinberg in virtually every case!
Generally, looking at the first set of examples, the last note (C) in the second group of four, the stem is too short! Ideally it should just fall short of the where the first leger line would be. As for the cross beaming it is, in the main very ugly! There are ways of making the notes look more even in appearance. When I was taught at Halstan to engrave by two old boys, who actually were engravers when they started out, as I understand it, their main ‘bible’ was Henle Editions.
Also, a beam should not slope more than a stave space.
@Bev: I agree that the note spacing in the cross-staff beaming case is far from ideal. We aren’t finished with spacing yet, by any means, so I would expect those kinds of beams to look much better when all is said and done.
Since the rules for 18-C beaming (the first Corelli example) appear to be so easily codified, it would be nice to have this as a style option for baroque music. It has a certain style and character that seems to me to be consonant wirth the music itself.
Thanks for this post. I just wanted to comment that there are beams in an engraved score by Luzzasco Luzzaschi published in 1601 (“per cantare, et sonare…”), but likely written in the 1580s. Here’s a screen shot.
He seems to just switch beam direction whenever necessary, and since (perhaps) slurs hadn’t been used for vocal music at the time we just have to go by the text underlay.
Thank you for sharing these detailed thoughts with us. I had never thought so intimately about details of placing and shaping beams before. It’s interesting to see that none of the existing programs is perfect, although (as others have commented) some of it is also a matter of taste or at least decision.
Now that I realize the necessity of the positioning of beam ends (so far I had only thought of the slope) I’m happy to see that my favourite product makes it extremely easy to do that right when one should need to position beams manually. When using integers to override a beam position the beam straddles on the given staff line, add or subtract 0.25 to that number and your beam perfectly hangs or sits on that line.
As usual on this blog, that sounds extremely promising, Daniel. The point about rotating beams is very interesting.
And now if you were tell us that beaming across multiple barlines and/or systems will also be handled gracefully (something that products A & B are not so good at), I’d be enchanted.
Looks very promising indeed! Can you indicate if the creation of more detailed subgroups will be possible? Here is just an example of what I mean. It is not ment as standard …. but for rhythmic clarity one might need things like this.
@Cees: Yes, absolutely. Those kinds of groupings will be no problem, and we plan to support stemlets, although we don’t have them implemented just yet.
@Robert: Beams over barlines and system breaks are absolutely supported in our application. Special care has been taken about establishing a consistent slope but independent height for the separate segments of beams that fall either side of a system break.
Thanks, Daniel.
Something that is probably obvious, but any default behavior of the new application can be tweaked locally (to the slightest detail) a la product B, right?
@Robert: Yes, you will be able to adjust the slope and slant of every beam individually to suit your taste or requirements.
While I agree with most of your comments, many serious engravers change the defaults of A and B to get more palatable results, and as you say, some of us use third party plugins to correct errant defaults. You might have a look at Boosey & Hawkes’ internal style guide (if they will let you) for beam treatment, which I think has the best looking beams I’ve seen (in Product D), avoiding wedges and floating beams, while maintaining acceptable stem lengths and pleasant slopes. (I prefer more gentle slopes than most of the examples above, like the first bar of the Schott example.)
One thing I should also suggest, and Product B does this to a certain extant (although not explicitly), is how to treat beam slopes relative to line contour. One publisher I work with asks for slopes if the musical line all goes the same direction. However, if a note repeats, or if the line turns, the beam should be flat. Hence, ABCD slopes up, ABCB is flat, as is ABCC. Yes, it results in a preponderance of flat beams (like product B), but it simplifies the process of avoiding wedges or stems that are too short. It works well with modern music, especially with lots of unusual beam groupings. While this shouldn’t be your default, it would be nice to have it as an option. (It can be a nightmare fixing them all in Product A.)
One other reason to include it is staff size. With smaller staff sizes, it is more difficult to avoid wedges, and sloped mid-space beams have a habit of merging with staff lines at both ends. Yes, you can thin the beams (effectively spreading multiple beams like in your last example), but after a certain point they are no longer discernible from staff lines. Personally, I find your spread beams unacceptable with the sloped beams (but OK when flat), and find Product D clearest in your example, though not following the rules as you state them. When you are dealing with scores of more than 35 staves, this becomes a significant problem, unless you are printing larger than A3/Ledger size.
@Stephen: The conditions you outline for when beams should be flat rather than sloped are pretty much exactly those that our application follows, with the exception of the ABCC figure (which would produce an upwards slope). I’ll talk to James (the developer whose hard work has made all of this beaming goodness possible) about this.
All this is very fine but would that leads us to a decent notation software soon ?
I have Cubase since 1.5 year and abandon using it because of its poor and overcomplicated notation software. I’m still waiting for one that will fit my musical needs, not my programming needs.
Feel free to reply at michel.jubinville@hotmail.ca
Thanks
@Michel: We’re going as fast as we can! We take the view that every detail is important, and we hope that our prospective users are willing to wait a little longer while we build something of a very high quality, with a solid foundation for future development.
From what I read, Steinberg is potentially an exciting new alternative to the current existing options which each have their own inherent weaknesses that we must adjust manually. It may be expecting too much to hope that this new software will successfully address all the problems, I hope they can. But for now I think we should allow them to work on the core standard notation models and get the thing working, rather than push and test them with unusual and non standard notations. Hopefully this will come in time, and maybe to the extent that we don’t need to use Illustrator for difficult scores. In the meantime, I’m really pleased to see they are addressing issues that in the existing softwares remain problematic. Good work. Keep going.
Daniel, it is always a great pleasure reading your blog posts, and I am so happy that you pay so much attention to all the details of music engraving. Thanks a lot! I am familiar with the beaming rules outlined by Stephen Ferre and I too would be happy to see an optional beaming style avoiding (most of, if not all) wedges and producing flat beams when the melodic line turns. You say that these are pretty much the rules used by your application, but in that case the 6th and 7th groups should have had a horizontal beam. I am aware that it is not everyone’s taste to do that, but could be an option?
Thank you Daniel. To be honest I’m not sure I like the look of the 64th note beams, I prefer the more compressed look of A. Good to hear cross-staff beam note spacing is being considered – that drives me nuts, especially when with accidentals.
Thanks Daniel, for taking the time to educate us. I feel like I’m getting a college course in engraving just from reading these blog posts! I do have one question related to the grace note beaming example: The second group of 4 beamed notes (Steinberg, D,E,E,F) appears to have a significantly steeper beam slope than the third group (D,E,F,G) despite having a smaller pitch interval from beginning to end. I’m not clear on which rule is resulting in that, nor why it would be desirable? From a player’s perspective, the steep pitch of the beam might tend to ‘hide’ the repeated pitch if not paying careful attention.
@Jeff: The D,E,E,F group would ideally have a slant of 0.75 spaces, but this would result in one end of the beam not being placed correctly relative to a stave line. It ends up with a slant of just under 1.25 spaces (under because the grace note beam is two-thirds thinner than a normal beam line) because this allows the stem tip at each end of the beam to have a valid placement. The D,E,F,G group would ideally have a slant of 1 space, and fortunately it is able to achieve this without adjusting either end of the beam. It’s not necessarily desirable that a beam group describing an interval of a third should end up with a slant greater than a beam group describing an interval of a fourth, but the best case scenario would perhaps be that the slant should be the same in this case.
Thanks, Daniel for yet another intriguing blog post! Correct and attractive beam placement is one of the major shortcomings of current scoring apps, and I find the Steinberg examples to be exactly what I would prefer by default, except for the quadruple beams example, where product C is closer to my preference. I completely agree with Fred’s thoughts on this.
Also, just curious, will so called ‘french beams’ (i.e., beams where the stem length doesn’t go beyond the lower secondary beam on inner notes) be available as an option in your application?
Anyway, with the option of tweaking settings for separate intervals and manual adjustment of beams, this is shaping up to be quite the contender in the beam department. I’m really looking forward to further updates on the progress!
@Knut: Regarding French beams, these will certainly be included at some point, though perhaps not in version 1.0. I can’t promise anything –– until it’s actually done and implemented, it’s always possible that something could happen to prevent us from doing so.
Hi Daniel,
I am really longing for you product whatever the price may be because it looks very promising. So far I use Product A for my piano Jazz transcriptions and I don’t have time to learn text input from Product C (which so far gives the better output IMHO)..
So, I am very impatient ….. your product is really what I am looking for : something that really focus on music notation.
I hope Steinberg will give you enough lattitude to work on your product and give us the ultimate music notation software !
So … I will wait
What about beams over bar lines? I trust this will be straight forward!
@Bill: Yes, beams over barlines present absolutely no problem at all.
We need a “Like” function on here! 🙂
well said Bill! 🙂
Daniel,
Any chance of note names inside of note heads, for us teachers out there?
Thank you!
@Andrei: I included note names within noteheads in the SMuFL specification, and I hope that we will be able to support this directly in our application in due course.
Thank yo, Daniel! Best wishes…
That’s great, especially if you don’t do it the Logic Pro way”, where it’s a simple on/off switch for all notes in a staff/clef, if it supports the Sibelius way where one can add note names on an individual note basis…. and it would be particularly great of one could define a ranges where note names inside note heads would appear. This would be useful for students who need them for notes eg in the very high and very high ranges only.
Thanks for your detailed analysis, Daniel!
Regarding the stubby note group in your example: the scoring deems that the disparity between ideal slope (-0.63 staffspace) and steinberg’s example is a worse tradeoff than the shortened stems for LilyPond’s choice. To be exact: the scoring for the steinberg choice is 2.57 (ideal slope) + 1.57 (stem) and the LilyPond choice gets 0.17 (slope) + 2.96 (stem length).
The scoring system inside Lily has a bunch of parameters that I picked without much thought, and tuned until they gave something reasonable. They could probably be tuned in an automated fashion so it gets even more configurations right. (genetic algorithms?)
Regarding the beam spacing for grace notes: I never gave it much thought: the thickness is reduced by 20%, and the scoring continues. The excessive space is a bug, I posted https://codereview.appspot.com/214250043/ to fix it.
While doing good on the examples you show here is important, I believe most programs are capable of doing a decent job at it. It becomes much more interesting if you throw collisions into the mix. Check out http://lilypond.org/doc/v2.19/input/regression/collated-files.pdf, and look for “beam-collision”. I’d be interested to see how products A-E and Steinberg do when there are clef changes, rests or accidentals under (possibly kneed) beams.
@Han-Wen: Thanks for your feedback. There are really very few objective criteria for judging beam placement, as I wrote in my blog post, and as has been borne out by some of the comments (with people e.g. expressing a preference for wedges over “correct” placement of stem tips). Every application approaches the problem in a different way.
Regarding resolving collisions of objects under beams, I don’t believe any of the products I have used in these comparisons other than our own application and Product C attempt any kind of collision avoidance for beam lines versus clefs, key signatures, accidentals, notes in other voices, etc.
When will you give the demo version of the application on the internet?
Thanks
I would imagine that securing the best on-board sound library would be priority number one from the Yamaha-Steinberg side. If at some point third-party sample libraries would be implemented, I was wondering what the approach might be to hide/show key switches for patch changes.
One notes that all of the Blog entries and almost all of the comments pertain only to the minutia of engraving, rather than the broader topic of music production or “music technology” in general. I presume that everyone here appreciated the importance of good engraving and appreciates the attention o those details.
However, one also hopes that if Steinberg is funding this project they would recognize the importance of seeing a strong, mostly seamless integration between DAW and notation such that composition could be done in either platform and be reflected in the other in real time. But in reading the various entries, I don’t get the sense that is a priority, or even a recognized need.
I hope I am wrong.
I very much agree with you. The large number of comments below this and other posts where users express their hopes and expectations of what future notation software should be capable of makes me think we are not the only ones. I recognize this is somewhat beyond the scope of this blog, but the importance of the topic also makes me post here.
I am, however, quite sure that Steinberg is very aware of the market situation and that they surely will follow a well-thought strategy.
They know that engraving quality is an absolute prerequisite for any success in the notation market, so this blog is a good starting point. Then comes completeness and usability. If a single important feature is missing, users will not change. If common tasks are not easier than with other notation software, users will not change. And then comes innovation – something I personally have not seen for a long time. So there is much that can be done. An integrated DAW-and-notation environment, while still preserving the DAW and the notation application on their owns, is such a game-changing innovation and so tempting for a company that has a very popular DAW software that I am confident Steinberg will not miss this opportunity. While engraving quality is the prerequisite, this will be their selling point.
best wishes 🙂
I didn’t comment on your reference to Yamaha and their recent acquisition of Steinberg. I don’t know that much about Steinberg, but it seems to me that most of the DAW companies are dominated by rockers and garage band types and some professional studio guys, none of whom have much of a priority on notated music. Yamaha, on the other hand, is very involved with the professional music community and the academic music community. My guess is that Yamaha is a bit more in tune with the convergence that is needed on the :”music technology” front, so this could be a good omen towards integrating DAW with notation, allowing the best playback while composing either in the DAW (interactively) or in the notation mode (traditional composition).
Any chance the new product will be called Spreadbury? 🙂
I keep throwing money at my computer and nothing happens… really looking forward to the release.
Hi Daniel,
Beams, schmeams – is there any ballpark timeline on when the product is going to be released? 2015, 2016, 2017???
And thank you for the great work!
Daniel Léo Simpson
Composer
San Francisco
Hi Daniel,
Great work as usual!
Are you planning on adding support for beaming across more than two staves?
And unrelated: Are you planning on adding support to custom staffs where a staff could have more than 5 lines, and where the staff lines can be spread unevenly. Are you planning on adding support to musical notation that have more than 7 note names per octave? (I’m a microtonal buff)
Best,
Michael
@Michael: Yes, you can beam across more than two staves very easily. We will no doubt eventually support staves with more or less than five lines, but it may not be something that makes it into the very first version of our software, as we have to prioritise! We do already have good support for microtonal accidentals and systems of tuning more advanced than 12-EDO or 24-EDO.
This is great great news! Thank you!!
It would be good if your new music notation program could support the input through the pen used in the Microsoft Surface Pro 3 and now Microsoft Surface 3. That would allow composers to write (input) music nearly as it they were doing on paper previously with a pencil but this time using a pen like the one used by the Surface 3 and Surface 3 Pro.
All the best wishes for your new music notation program.
Please buy “staffpad” and integrate its pen input in your application!
Michael
I have been so swamped lately that here I am, commenting on this fine blog entry a whole month after it is posted.
One thing about cross-beaming that I find is lacking amongst notation programs, is actual cross-instrument beaming, as is sometimes seen in the percussion parts of French-published scores. Cross-beaming is generally used for a single keyboard instrument, and this is how it is understood by commercial products at the moment. Notating this example for Milhaud’s “La création du monde” however, is currently impossible on the software I currently use:
https://www.dropbox.com/s/cmb8dj5z2uoabod/darius.png?dl=0
I realize that there are other ways of notating this, but this example of cross-instrument beaming is actually quite attractive and clear. Is this something that would be implemented in the Steinberg product?
I know this blog is about Steinberg (so no flaming please), but you should know that LilyPond can do cross-instrument beaming without a second thought. It took me a only a couple of minutes to do this.
Thanks! You do learn something everyday!
Yeah, you should really get involved with the staffpad people.
Hello,
It would be great if your new app could somehow integrate or interoperate with this pure diamond software called staffpad.
Sibelius has integrated the staffpad to the new version. 🙁
@ercan: I don’t think so, not in the least. I haven’t seen the new update myself yet, of course, but the way I interpret the support for the Surface Pen in the new version is that you will use it as a mouse, i.e. you will tap on the Keypad the note value etc. you want, then tap with the Pen at the position where you want to input a note, but you won’t actually be able to write the notes in freehand.
I can confirm that, according to Andrew Wild interview, new Sibelius version will have handwritten notation and notes regognition on Surface Pro :
@Alain: You’re not watching that video very closely! Take a look at the 2:08 mark, where you can clearly see notes being input not by handwriting them, but only by touching the pen to the staff at the position where the note is entered. In the few seconds before that, you can see somebody drawing some slur-like lines freehand, but the software doesn’t convert them into actual slur objects in the score: it’s just freehand annotation using the pen.
Note that it has been announced that Neuratron will be releasing an updated version of PhotoScore Lite including their NotateMe Now technology, alongside this update, which will allow handwriting input into PhotoScore, but this is a separate application. You will be able to write music by hand into PhotoScore and then send it to Sibelius, but you could also send that music to any other music application via MusicXML, just as you can with the current versions of NotateMe for iOS and Android (which, incidentally, also include PhotoScore as an in-app purchase).
I would suggest you take a more sceptical view and wait and see what kind of pen support is included in this update. It took the team behind StaffPad three years, working full-time, to come up with the handwritten music recognition in their application, and one of the developers of that product (Matt Tesch, of Google) had prior experience working in this area. Neuratron, who produce NotateMe for iOS and Android, have been working on handwritten music recognition for ten years. I don’t doubt that there are talented developers working on Sibelius, but I am highly sceptical that they will have been able to match the efforts of more experienced developers with specialist expertise in the field of music handwriting recognition in a fraction of the time.
Hi Daniel, surely my question has been answered before, but I couldn’t find it,… so : I wonder what will be an integration of the new notation software with Cubase (8).Will it replace Cubase’s poor notation editor, or will it be functional as VST plugin (perhaps as a sequencer plugin) or running in a rewired mode? I really hope it can somehow integrate with Cubase DAW so we can have a tool that utilizes both elements: a composition (structural writing) and a production (sonic development). I always believed that music notation is a phenomenal invention since it contains a lot of music information in very little space (in comparison to a silly piano roll etc. alternatives). I keep on struggling to rewire Sibelius, Cubase and East West ( something always crashes) hoping that one day (sooon?) we will get something useful. Sibelius and Pro tools are working that direction so we really hope you guys could deliver something much nicer.
@Vlado: At first, our new application will be completely separate from Cubase, though our scoring application will include Cubase’s audio engine, so it will have the same high-performance, high-quality audio output, including full VST3 support. Over time, we will look for opportunities to integrate the technologies in the two products more closely, and this may include improvements to Cubase’s score editor itself, or allowing the two applications to work together. We have a lot of foundational work to do first, however, so please don’t expect tight integration between Cubase and our scoring application in our very first release.
HI Daniel
When you are done with Steinberg, can you please move to Cupertino (or Hamburg), and create a similar program for Logic (and improve Logic’s woeful score edit functions). 😉
They wrote here. Sorry İ dont know much Englih. 🙁
http://www.sibeliusblog.com/news/next-sibelius-release/
Hi Daniel! I just saw this post and it warms my heart to see how seriously you’re taking beaming (although by this point, I’ve stopped being surprised). I wanted to flag a particular use case for you.
https://www.dropbox.com/s/0rbwtgb0go8bavr/64th%20beaming.png?dl=0
Your cross staff beams should be able to handle interior beam breaks gracefully. In the above example, there are several niceties that were observed:
64th beams broken: the 64th and 32nd beams were broken to show the proper grouping of 64th notes. Sibelius doesn’t allow preferentially breaking secondary beams (please include this!).
Primary beam manipulation: to avoid beam corners, the primary beam needed to be shifted for each group. I started with the interior two groups: their primary beam is the one that needed to look right. For the outer groups, the middle group’s primary beam becomes the 16th beam and the 16th beam in the interior group becomes the primary for the outer.
This situation doesn’t come up very often, but I thought I would share my solution.
Also: a couple of years ago, I made this poster for myself. I have it next to my workstation for reference and have found it very useful.
https://www.dropbox.com/s/50tmzx3aoxa4rzu/Beam%20Slant%20poster.pdf?dl=0
Thanks,
Matthew
@Matthew: I love your big Ross poster. Did you change any of the slants from how they were printed in his book? As I think I wrote in the blog post, there are some frustratingly unexplained inconsistencies between apparently identical slants in the book’s tables. I’d be curious to know if you have spent any time trying to work through them, as we have, and what conclusions you drew, if any. Our application neither produces exactly the slants that Ross gives in every situation, and nor does it use the kind of table-based approach of rules (for this starting and ending note, the slant is this; for this starting and ending note, the slant is that; etc.) that would allow you to spend a day typing them all in and then producing exactly those slants. But we are broadly following Ross’s principles, and I hope you’ll be happy enough with them.
Regarding your beam grouping example, that happens to match exactly an example given by Gould in Behind Bars (top of page 157) in terms of how the beam breaks should be handled. At the moment, our algorithm doesn’t produce exactly this result (it doesn’t use a single primary beam to join the two halves of the beam group that each add up to one eighth or quaver), but James, who has been slaving away on beams for quite some time now (though he has taken a break for a few weeks to turn his attention elsewhere just at the moment), has plans to improve the algorithm such that it will do so. Assuming you have secondary beam breaks after each group of four 64th notes, our application will correctly position each of the sub-groups on the correct side of the primary beam in a between-staves context, as shown in your example.
Our algorithm also has special handling to avoid beam corners, which it does considerably more successfully than certain other commercial scoring applications.
Hi Daniel: I’m glad you like my poster. I didn’t try to resolve any of the inconsistencies. There are differences throughout the book as well. I figured that when he was doing the example pages, he was largely going by feel while keeping the guidelines in mind. As with so many things in engraving, looking right is often better than actually being right from a theoretical perspective. Frankly, close enough here is perfectly fine. I’m sure the compromises you’ve made with your algorithm are good.
For cross staff beaming: Sibelius’ solution is to have the beam anchored to the midpoint between staves. Positioning it accurately and having it stick is difficult. The distance between staves changes often enough that I need to wait until the end of editing to make final adjustments. Major kudos to you and your team though for making beam adjustments in increments of 1/4 space though.
I’d like to propose the following behavior for cross staff beam positioning:
Slant: if the individual groups would all be beamed with the same slant, the larger beam should be slanted that direction between 1-2 spaces. If the individual groups would have different or flat slants, the larger beam should be flat.
Vertical position: take the two shortest stems in the group and make them roughy equal. Ideally, they shouldn’t be shorter than 2.5 spaces, but I doubt achieving that automatically would be appropriate as it would shift the rest of the layout.
If the beam overlaps one of the staves, it should conform to standard positioning with the stafflines.
If the staves are moved, beams should move with them. However, there should be the ability to lock the beam with reference to one of the member staves.
It would also be great for cross staff beams to be horizontally spaced by their stems when no other instruments are playing simultaneously.
More important that the automatic solution is the ability to make edits that stick and don’t have to be continually monitored.
Keep fighting the good fight. Thank you so much for your work, especially now that the new Sibelius devs have clearly signaled the direction in which they’re taking the software.
@Matthew: In broad strokes, your proposal for the handling of slants and vertical positioning for beams between staves is more or less what we’ve got implemented. There are still a number of details for us to address, but I’m pretty confident you will be happy with what we come up with.
The example notation from John Johnson ( 1720) displaying musical informations (from my viewpoint) best of all 😉 . All other notation writings from modern times has his typical digital borders and geometry. John Johnson but had a organical window to the build of music, not more displayed after 20. century.
Thanks alot.. this is really good information. But i will be totally honest. I personally dont care about beams and where they are placed LOL but i would care about making the connection between the libraries articulations and the notes better. That whole thing seems to be a big cluster. im personally stuck in my musical world right now. I hate writing music in a DAW window but i know its the best way to use great sounding instruments. I prefer to writing in sibelius where i can see the notes but the sounds are annoying then you have to export it and get everything lined up in the DAW.. it makes me not want to right anymore. I would rather see advancements in that before notes
Building an excellent notation program in a post-Finale-post-Sibelius world takes time. That’s why we trust Daniel and his team to get it right.
“The art of making art Is putting it together, bit by bit, beat by beat, part by part, sheet by sheet, chart by chart…” ~Stephen Sondheim.
Another nut to crack along the way will be non-standard Key Signatures to included microtonal. Not only the notational aspect and ease thereof but playback.
This will place it far and above both Sibelius and Finale.
if we want , can we use your application instead cubase standard notation? or will cubase
offer an option to use new application? (if the new application setup on the computer).
@ercan: Our new application and Cubase are completely independent, at least for the time being. As our application matures, we hope to build meaningful integration between our application and Cubase.
Thank you Daniel for your wonderful blog posts. I am not an engraving nerd, but I really enjoyed the latest one.
My personal feedback on your first example, simply as an average kind of musician, is that three things immediately leapt out at me.
– your new product produces a lower beam than the Schott edition for the second group of four quavers in bar 1. This looks aesthetically wrong to me. I’m wondering if it’s because of the D in the first group of four quavers, which in some way is clashing with the beam on the second group of four in your product. It feels better to me if the beam in the second group is higher than all the notes in the bar, as per the Schott version.
– exactly the same thing happens in the last group of four quavers in bar 4, and maybe for the same reason
– in the last note of bar 3, your stem is very short. The Schott edition has a longer stem and this definitely feels more familiar and right to me. It makes it easier to ‘see’ the octave between the A’s and the leap to the D at the beginning of the next bar.
best wishes,
Rich
can we use your application with all Steinberg VST-VSTI?
@ercan: Yes, our application will support the same VST instruments and effects as Cubase.
This is way late, and I’m not sure if anyone is still reading comments (and perhaps I missed this in another post), but one important thing about beaming comes in tremolo notation – specifically, slashes through the stem, of beam thickness. In many editions, tremolo slashes are drawn parallel to the main beam(s) when they occur on beamed notes. Product C does this by default (see my avatar), but neither of the two leading commercial programs is even capable of it without a great deal of heartache. In Behind Bars, Gould suggests that the commercial programs have it correct for current standards and that parallel-to-beam tremolo marks are obsolete. Any thoughts on this? Perhaps incorporate both and let the user choose which style to use?
@Another Matt: Thanks for your thoughts on this. We haven’t yet started looking at tremolos, but I will certainly consider whether we can support both angled tremolos and tremolos that are parallel to the beam.
Great thanks on this articles! Been spending months to develop musical notation crazily thank to beaming and assume there was some rules to follow. Look like it appear differently across software and even on MIDI keyboard display itself.
H Daniel,
Regarding the beams rotating instead of shearing, how do you handle a multiple beam? Does the entire stack of beams rotate, to maintain the same distance between them as well as the same thickness for each? Or does the rotating effect only apply for single beams?
@Isaac: I think on balance I’ve given enough assistance to Product E’s developers over the past few years already, haven’t I? But yes, all beam lines are rotated when there is more than one beam line.
Indeed, your blog posts, and particularly the direct comparisons and criticisms of output, have been very much appreciated at Product E. (Not to mention Bravura.) Keep leading by example, and we wish you the best and a terrific launch for Dorico.